FAQs

This task is not quite so simple. There are in fact many methods for solving rational equations, and about a hundred of these methods are used in our program. Try, for example to solve the following equations:
x⁴=(x+1)(5x²-6x-6)
(1+x+x²)⁴=(1+x²+x⁴)²
(x²+1)²(x+1)=0.8
UMS solves rational, irrational, logarithmic, exponential and trigonometric equations.

To input the simultaneous equations, click the { button and enter each of the equations on a separate line. To add the next equation, press the Enter button.

The UMS program considers this expression to already be in the simplest possible form. We recommend you select “Expand” in the “Mathematical Subject” menu.

The argument of the entered function must be enclosed in parentheses. For example f(x) = x² – x³ or y(x) = x² – x³, or the argument can be omitted, for example y = x² – x³. In this case UMS would consider the expression as a function.

We recommend you select “Complete factoring” in the “Mathematical Subject” menu.

This example does not allow for a precise solution. UMS is designed to find precise results (perhaps in radicals), but not approximate ones.

You need to use the quadratic function y = x² + px + q: The graph of this function is a parabola with branches pointing up.

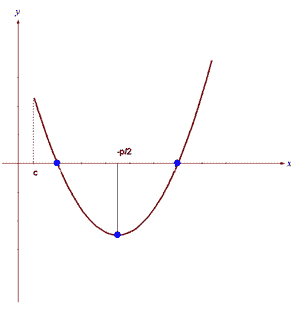
The Vertex of the parabola has an x-axis value of x = – p/2. In your example p = – 6a, x= – p/2 = 3a. In order for both roots of the quadratic function to be greater than some number c, it is necessary and sufficient for the system of three inequalities to be true:

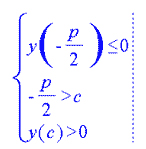
In your example this system will look like this:

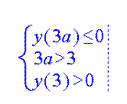
Or

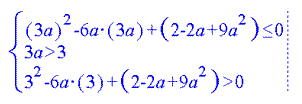
This system of inequalities can be solved using UMS.

The equation was not written correctly. In your equation log(x) is raised to the square and to the fourth degree. If we write this equation in the form: log(x) + log(x²) + log(x⁴) = 7, then argument x is raised to the square and to the fourth degree. Now UMS can solve this simple equation.

In order to find the value F(c) of a function F=f(x) for the given value of variable x=c enter the following system and solve it with UMS.

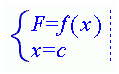
In your example this system will look like this:

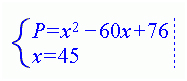
UMS solves this system and receives:

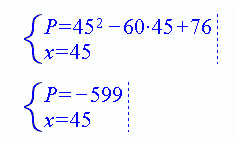
that is P(45) = -599

You forgot to enter the degree sign. You must enter

Now UMS solves this problem and gives the right answer -1/2.

Free Algebra Equation Solver is our regular Universal Math Solver software with “Equations” section enabled for free. It does not require a license or any type of registration whatsoever in order to solve your equations and systems of equations. However, if you try to solve a user defined problem from other topics like for example Inequalities or Factoring it will ask for a license. You can still demo step by step solutions from other sections by selecting a problem from the main Collection. Please make sure you enter equations or systems of equations only if you want to use the free version.

You may have to re-install the UMS software using Administrator account. Once it is installed, you can run it under a regular User account.

We assure you that there are no valid cracks for the Universal Math Solver software. Best case scenario you will get a number that is actually a valid license. It may or may not work depending on that license expiration date and number of prior installations. Worst case scenario you will get a virus. Please download only from our site, CNET Download site or Software Informer site. Free Algebra Equation Solver is free as the name implies and does not require any license or code.